A simple pendulum consists of a relatively massive object hung by a
string from a fixed support. It typically hangs vertically in its
equilibrium position. The massive object is affectionately referred to
as the
pendulum bob. When the bob is displaced from equilibrium
and then released, it begins its back and forth vibration about its
fixed equilibrium position. The motion is regular and repeating, an
example of periodic motion.
we learned that an object that is vibrating is acted upon by a
restoring force. The restoring force causes the vibrating object to slow
down as it moves away from the equilibrium position and to speed up as
it approaches the equilibrium position. It is this restoring force that
is responsible for the vibration. So what forces act upon a pendulum
bob? And what is the restoring force for a pendulum? There are two
dominant forces acting upon a pendulum
bob at all times during
the course of its motion. There is the force of gravity that acts
downward upon the bob. It results from the Earth's mass attracting the
mass of the bob. And there is a tension force acting upward and towards
the pivot point of the pendulum. The tension force results from the
string pulling upon the
bob of the pendulum. In our discussion, we will
ignore
the influence of air resistance - a third force that always opposes the
motion of the bob as it swings to and fro. The air resistance force is
relatively weak compared to the two dominant forces.
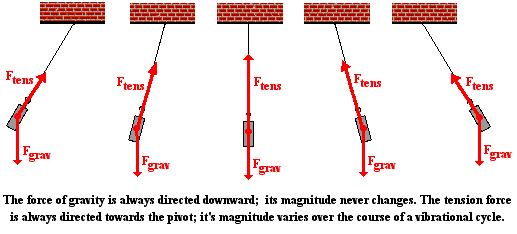
The gravity force is highly predictable; it is
always in the same direction (down) and always of the same magnitude -
mass*9.8 N/kg. The tension force is considerably less predictable. Both
its direction and its magnitude change as the bob swings to and fro. The
direction of the tension force is always towards the pivot point. So as
the bob swings to the left of its equilibrium position, the tension
force is at an angle - directed upwards and to the right. And as the bob
swings to the right of its equilibrium position, the tension is
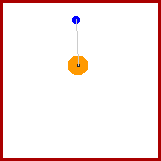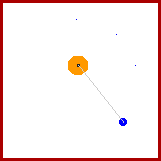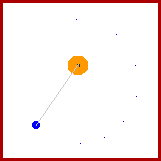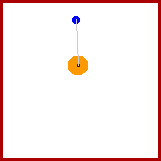
directed upwards and to the left. The diagram below depicts the
direction of these two forces at five different positions over the
course of the pendulum's path.
In
physical situations in which the forces acting on an object are not in
the same, opposite or perpendicular directions, it is customary to
resolve one or more of the forces into components. This was the
practice used in the analysis of
sign hanging problems and
inclined plane problems.
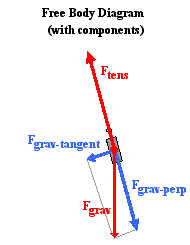
Typically one or more of the forces are resolved into perpendicular
components that lie along coordinate axes that are directed in the
direction of the acceleration or perpendicular to it. So in the case of a
pendulum, it is the gravity force which gets resolved since the tension
force is already directed perpendicular to the motion. The diagram at
the right shows the pendulum bob at a position to the right of its
equilibrium position and midway to the point of maximum displacement. A
coordinate axis system is sketched on the diagram and the force of
gravity is resolved into two components that lie along these axes. One
of the components is directed tangent to the circular arc along which
the pendulum bob moves; this component is labeled Fgrav-tangent. The
other component is directed perpendicular to the arc; it is labeled
Fgrav-perp. You will notice that the perpendicular component of gravity
is in the opposite direction of the tension force. You might also
notice that the tension force is slightly larger than this component of
gravity. The fact that the tension force (Ftens) is greater than the
perpendicular component of gravity (Fgrav-perp) means there will be a
net force which is perpendicular to the arc of the bob's motion. This
must be the case since we expect that
objects that move along circular paths will experience an inward or centripetal force.
The tangential component of gravity (Fgrav-tangent) is unbalanced by
any other force. So there is a net force directed along the other
coordinate axes. It is this tangential component of gravity which acts
as the restoring force. As the pendulum bob moves to the right of the
equilibrium position, this force component is directed opposite its
motion back towards the equilibrium position.
The above analysis applies for a single location
along the pendulum's arc. At the other locations along the arc, the
strength of the tension force will vary. Yet the process of resolving
gravity into two components along axes that are perpendicular and
tangent to the arc remains the same. The diagram below shows the results
of the force analysis for several other positions.
There are a couple comments to be made. First,
observe the diagram for when the bob is displaced to its maximum
displacement to the right of the equilibrium position. This is the
position in which the pendulum bob momentarily has a velocity of 0 m/s
and is changing its direction. The tension force (Ftens) and the
perpendicular component of gravity (Fgrav-perp) balance each other. At
this instant in time, there is no net force directed along the axis that
is perpendicular to the motion. Since the motion of the object is
momentarily paused, there is no need for a centripetal force.
Second, observe the diagram for when the bob is at the equilibrium
position (the string is completely vertical). When at this position,
there is no component of force along the tangent direction. When moving
through the equilibrium position, the restoring force is momentarily
absent. Having been
restored to the equilibrium position,
there is no restoring force. The restoring force is only needed when
the pendulum bob has been displaced away from the equilibrium position.
You might also notice that the tension force (Ftens) is greater than
the perpendicular component of gravity (Fgrav-perp) when the bob moves
through this equilibrium position. Since the bob is in motion along a
circular arc, there must be a net centripetal force at this position.
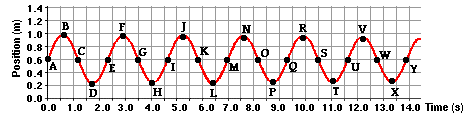
The Sinusoidal Nature of Pendulum Motion
In
the previous part of this lesson,
we investigated the sinusoidal nature of the motion of a mass on a
spring. We will conduct a similar investigation here for the motion of a
pendulum bob. Let's suppose that we could measure the amount that the
pendulum bob is displaced to the left or to the right of its equilibrium
or rest position over the course of time. A displacement to the right
of the equilibrium position would be regarded as a positive
displacement; and a displacement to the left would be regarded as a
negative displacement. Using this reference frame, the equilibrium
position would be regarded as the zero position. And suppose that we
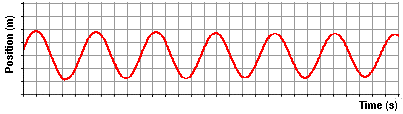
constructed a plot showing the variation in position with respect to
time. The resulting position vs. time plot is shown below. Similar to
what was observed for the mass on a spring, the position of the pendulum
bob (measured along the arc relative to its rest position) is a
function of the sine of the time.
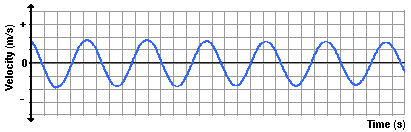
Now suppose that we use our motion detector to
investigate the how the velocity of the pendulum changes with respect to
the time. As the pendulum bob does
the back and forth, the
velocity is continuously changing. There will be times at which the
velocity is a negative value (for moving leftward) and other times at
which it will be a positive value (for moving rightward). And of course
there will be moments in time at which the velocity is 0 m/s. If the
variations in velocity over the course of time were plotted, the
resulting graph would resemble the one shown below.
Now let's try to understand the relationship between
the position of the bob along the arc of its motion and the velocity
with which it moves. Suppose we identify several locations along the
arc and then relate these positions to the velocity of the pendulum bob.
The graphic below shows an effort to make such a connection between
position and velocity.
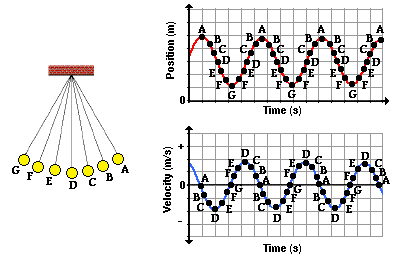
As is often said, a picture is worth a thousand words. Now here come
the words. The plot above is based upon the equilibrium position (D)
being designated as the zero position. A displacement to the left of the
equilibrium position is regarded as a negative position. A displacement
to the right is regarded as a positive position. An analysis of the
plots shows that the velocity is least when the displacement is
greatest. And the velocity is greatest when the displacement of the bob
is least. The further the bob has moved away from the equilibrium
position, the slower it moves; and the closer the bob is to the
equilibrium position, the faster it moves. This can be explained by the
fact that as the bob moves away from the equilibrium position, there is a
restoring force that opposes its motion. This force slows the bob down.
So as the bob moves leftward from position D to E to F to G, the force
and acceleration is directed rightward and the velocity decreases as it
moves along the arc from D to G. At G - the maximum displacement to the
left - the pendulum bob has a velocity of 0 m/s. You might think of the
bob as being
momentarily paused and ready to change its
direction. Next the bob moves rightward along the arc from G to F to E
to D. As it does, the restoring force is directed to the right in the
same direction as the bob is moving. This force will accelerate the bob,
giving it a maximum speed at position D - the equilibrium position. As
the bob moves past position D, it is moving rightward alo
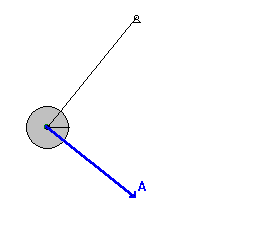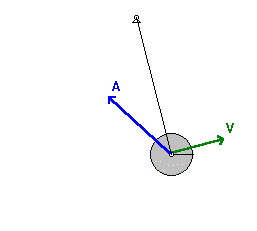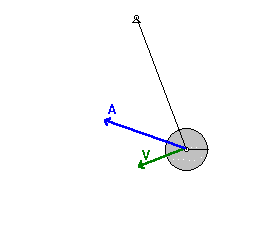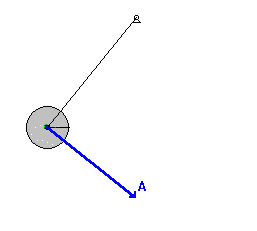
ng
the arc towards C, then B and then A. As it does, there is a leftward
restoring force opposing its motion and causing it to slow down. So as
the displacement increases from D to A, the speed decreases due to the
opposing force. Once the bob reaches position A - the maximum
displacement to the right - it has attained a velocity of 0 m/s. Once
again, the bob's velocity is least when the displacement is greatest.
The bob completes its cycle, moving leftward from A to B to C to D.
Along this arc from A to D, the restoring force is in the direction of
the motion, thus speeding the bob up. So it would be logical to
conclude that as the position decreases (along the arc from A to D), the
velocity increases. Once at position D, the bob will have a zero
displacement and a maximum velocity. The velocity is greatest when the
displacement is least. The animation at the right (used with the
permission of
Wikimedia Commons;
special thanks to Hubert Christiaen) provides a visual depiction of
these principles. The acceleration vector that is shown combines both
the perpendicular and the tangential accelerations into a single vector.
You will notice that this vector is entirely tangent to the arc when
at maximum displacement; this is consistent with the force analysis
discussed above. And the vector is vertical (towards the center of the
arc) when at the equilibrium position. This also is consistent with the
force analysis discussed above.
Energy Analysis
In
a previous chapter
of The Physics Classroom Tutorial, the energy possessed by a pendulum
bob was discussed. We will expand on that discussion here as we make an
effort to associate the motion characteristics described above with the
concepts of
kinetic energy,
potential energy and
total mechanical energy.
The
kinetic energy
possessed by an object is the energy it possesses due to its motion.
It is a quantity that depends upon both mass and speed. The equation
that relates kinetic energy (
KE) to mass (
m) and speed (
v) is
KE = ½•m•v2
The faster an object moves, the more kinetic energy that it will
possess. We can combine this concept with the discussion above about how
speed changes during the course of motion. This blending of concepts
would lead us to conclude that the kinetic energy of the pendulum bob
increases as the bob approaches the equilibrium position. And the
kinetic energy decreases as the bob moves further away from the
equilibrium position.
The
potential energy
possessed by an object is the stored energy of position. Two types of
potential energy are discussed in The Physics Classroom Tutorial -
gravitational potential energy and elastic potential energy. Elastic
potential energy is only present when a spring (or other elastic medium)
is compressed or stretched. A simple pendulum does not consist of a
spring. The form of potential energy possessed by a pendulum bob is
gravitational potential energy. The amount of gravitational potential
energy is dependent upon the mass (
m) of the object and the height (
h) of the object. The equation for gravitational potential energy (
PE) is
PE = m•g•h
where
g represents the gravitational
field strength (sometimes referred to as the acceleration caused by
gravity) and has the value of 9.8 N/kg.
The height of an object is expressed relative to some arbitrarily assigned
zero level.
In other words, the height must be measured as a vertical distance
above some reference position. For a pendulum bob, it is customary to
call the lowest position the reference position or the zero level. So
when the bob is at the equilibrium position (the lowest position), its
height is zero and its potential energy is 0 J. As the pendulum bob does
the back and forth, there are times during which the bob is
moving away from the equilibrium position. As it does, its height is
increasing as it moves further and further away. It reaches a maximum
height as it reaches the position of maximum displacement from the
equilibrium position. As the bob moves towards its equilibrium position,
it decreases its height and decreases its potential energy.
Now let's put these two concepts of kinetic energy
and potential energy together as we consider the motion of a pendulum
bob moving along the arc shown in the diagram at the right. We will use
an
energy bar chart
to represent the changes in the two forms of energy. The amount of
each form of energy is represented by a bar. The height of the bar is
proportional to the amount of that form of energy. In addition to the
potential energy (
PE) bar and kinetic energy (
KE) bar, there is a third bar labeled
TME. The TME bar represents the total amount of mechanical energy possessed by the pendulum bob. The
total mechanical energy
is simply the sum of the two forms of energy – kinetic plus potential
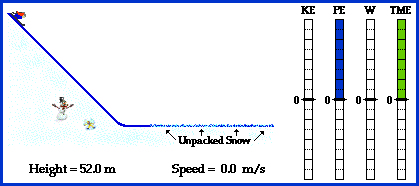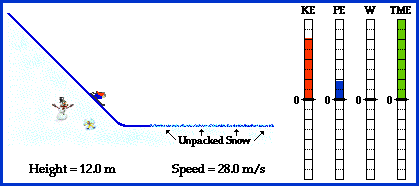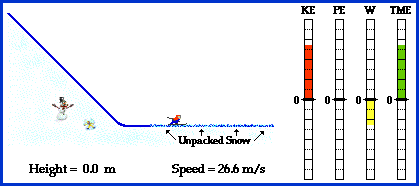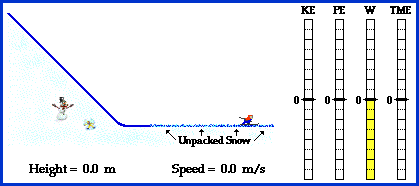
energy. Take some time to inspect the bar charts shown below for
positions A, B, D, F and G. What do you notice?
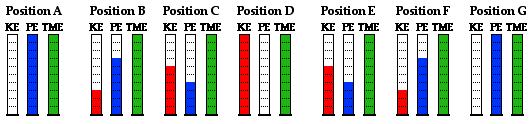
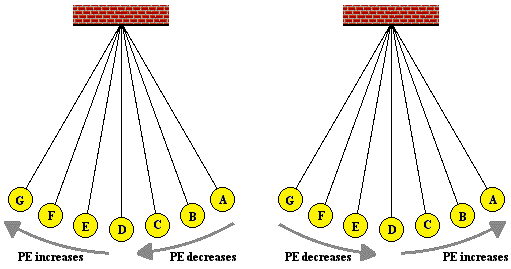
When you inspect the bar charts, it is evident that
as the bob moves from A to D, the kinetic energy is increasing and the
potential energy is decreasing. However, the total amount of these two
forms of energy is remaining constant. Whatever potential energy is lost
in going from position A to position D appears as kinetic energy.
There is a transformation of potential energy into kinetic energy as the
bob moves from position A to position D. Yet the total mechanical
energy remains constant. We would say that mechanical energy is
conserved. As the bob moves past position D towards position G, the
opposite is observed. Kinetic energy decreases as the bob moves
rightward and (more importantly) upward toward position G. There is an
increase in potential energy to accompany this decrease in kinetic
energy. Energy is being transformed from kinetic form into potential
form. Yet, as illustrated by the
TME bar, the total amount of mechanical energy is conserved. This very principle of energy conservation was explained in the
Energy chapter of The Physics Classroom Tutorial.
The Period of a Pendulum
Our final discussion will pertain to the period of the pendulum. As discussed
previously in this lesson,
the period is the time it takes for a vibrating object to complete its
cycle. In the case of pendulum, it is the time for the pendulum to start
at one
extreme, travel to the opposite
extreme, and then return to the original location. Here we will be interested in the question
What variables affect the period of a pendulum?
We will concern ourselves with possible variables. The variables are
the mass of the pendulum bob, the length of the string on which it
hangs, and the
angular displacement. The angular displacement or
arc angle
is the angle that the string makes with the vertical when released from
rest. These three variables and their effect on the period are easily
studied and are often the focus of a physics lab in an introductory
physics class. The data table below provides representative data for
such a study.
Trial
|
Mass (kg)
|
Length (m)
|
Arc Angle (°)
|
Period (s)
|
1
|
0.02-
|
0.40
|
15.0
|
1.25
|
2
|
0.050
|
0.40
|
15.0
|
1.29
|
3
|
0.100
|
0.40
|
15.0
|
1.28
|
4
|
0.200
|
0.40
|
15.0
|
1.24
|
5
|
0.500
|
0.40
|
15.0
|
1.26
|
6
|
0.200
|
0.60
|
15.0
|
1.56
|
7
|
0.200
|
0.80
|
15.0
|
1.79
|
8
|
0.200
|
1.00
|
15.0
|
2.01
|
9
|
0.200
|
1.20
|
15.0
|
2.19
|
10
|
0.200
|
0.40
|
10.0
|
1.27
|
11
|
0.200
|
0.40
|
20.0
|
1.29
|
12
|
0.200
|
0.40
|
25.0
|
1.25
|
13
|
0.200
|
0.40
|
30.0
|
1.26
|
In trials 1 through 5, the mass of the bob was
systematically altered while keeping the other quantities constant. By
so doing, the experimenters were able to investigate the possible effect
of the mass upon the period. As can be seen in these five trials,
alterations in mass have little effect upon the period of the pendulum.
In trials 4 and 6-9, the mass is held constant at 0.200 kg and the
arc angle is held constant at 15°. However, the length of the pendulum
is varied. By so doing, the experimenters were able to investigate the
possible effect of the length of the string upon the period. As can be
seen in these five trials, alterations in length definitely have an
effect upon the period of the pendulum. As the string is lengthened, the
period of the pendulum is increased. There is a direct relationship
between the period and the length.
Finally, the experimenters investigated the possible effect of the
arc angle upon the period in trials 4 and 10-13. The mass is held
constant at 0.200 kg and the string length is held constant at 0.400 m.
As can be seen from these five trials, alterations in the arc angle
have little to no effect upon the period of the pendulum.
So the conclusion from such an experiment is that
the one variable that effects the period of the pendulum is the length
of the string. Increases in the length lead to increases in the period.
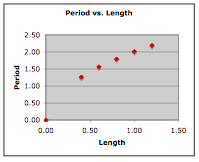
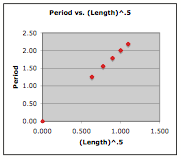
But the investigation doesn't have to stop there. The quantitative
equation relating these variables can be determined if the data is
plotted and linear regression analysis is performed. The two plots
below represent such an analysis. In each plot, values of period (the
dependent variable) are placed on the vertical axis. In the plot on the
left, the length of the pendulum is placed on the horizontal axis. The
shape of the curve indicates some sort of power relationship between
period and length. In the plot on the right, the square root of the
length of the pendulum (length to the ½ power) is plotted. The results
of the regression analysis are shown.
|
|
|
Slope: 1.7536
Y-intercept: 0.2616
COR: 0.9183
|
Slope: 2.0045
Y-intercept: 0.0077
COR: 0.9999
|
The analysis shows that there is a better fit of
the data and the regression line for the graph on the right. As such,
the plot on the right is the basis for the equation relating the period
and the length. For this data, the equation is
Period = 2.0045•Length0.5 + 0.0077
Using
T as the symbol for period and
L as the symbol for length, the equation can be rewritten as
T = 2.0045•L0.5 + 0.0077
The commonly reported equation based on theoretical development is
T = 2•π•(L/g)0.5
where
g is a constant known as the
gravitational field strength or the acceleration of gravity (9.8 N/kg).
The value of 2.0045 from the experimental investigation agrees well with
what would be expected from this theoretically reported equation.
Substituting the value of
g into this equation, yields a proportionality constant of 2π/g
0.5, which is 2.0071, very similar to the 2.0045 proportionality constant developed in the experiment.
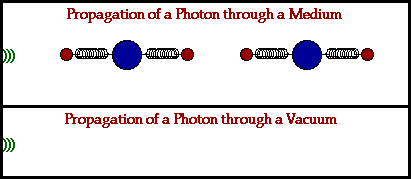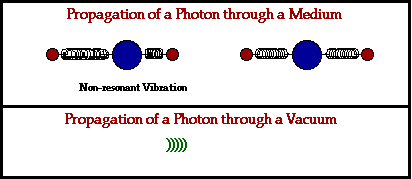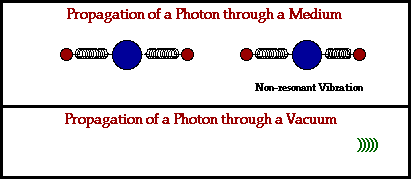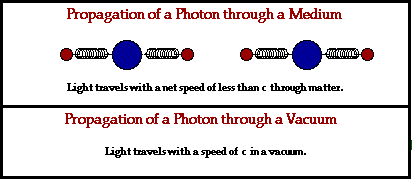 The actual speed of an electromagnetic wave through a material medium
is dependent upon the optical density of that medium. Different
materials cause a different amount of delay due to the absorption and
reemission process. Furthermore, different materials have their atoms
more closely packed and thus the amount of distance between atoms is
less. These two factors are dependent upon the nature of the material
through which the electromagnetic wave is traveling. As a result, the
speed of an electromagnetic wave is dependent upon the material through
which it is traveling.
The actual speed of an electromagnetic wave through a material medium
is dependent upon the optical density of that medium. Different
materials cause a different amount of delay due to the absorption and
reemission process. Furthermore, different materials have their atoms
more closely packed and thus the amount of distance between atoms is
less. These two factors are dependent upon the nature of the material
through which the electromagnetic wave is traveling. As a result, the
speed of an electromagnetic wave is dependent upon the material through
which it is traveling.




 In
physical situations in which the forces acting on an object are not in
the same, opposite or perpendicular directions, it is customary to
resolve one or more of the forces into components. This was the
practice used in the analysis of
In
physical situations in which the forces acting on an object are not in
the same, opposite or perpendicular directions, it is customary to
resolve one or more of the forces into components. This was the
practice used in the analysis of 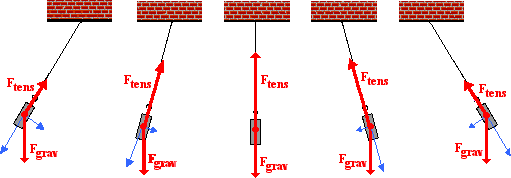



 ng
the arc towards C, then B and then A. As it does, there is a leftward
restoring force opposing its motion and causing it to slow down. So as
the displacement increases from D to A, the speed decreases due to the
opposing force. Once the bob reaches position A - the maximum
displacement to the right - it has attained a velocity of 0 m/s. Once
again, the bob's velocity is least when the displacement is greatest.
The bob completes its cycle, moving leftward from A to B to C to D.
Along this arc from A to D, the restoring force is in the direction of
the motion, thus speeding the bob up. So it would be logical to
conclude that as the position decreases (along the arc from A to D), the
velocity increases. Once at position D, the bob will have a zero
displacement and a maximum velocity. The velocity is greatest when the
displacement is least. The animation at the right (used with the
permission of
ng
the arc towards C, then B and then A. As it does, there is a leftward
restoring force opposing its motion and causing it to slow down. So as
the displacement increases from D to A, the speed decreases due to the
opposing force. Once the bob reaches position A - the maximum
displacement to the right - it has attained a velocity of 0 m/s. Once
again, the bob's velocity is least when the displacement is greatest.
The bob completes its cycle, moving leftward from A to B to C to D.
Along this arc from A to D, the restoring force is in the direction of
the motion, thus speeding the bob up. So it would be logical to
conclude that as the position decreases (along the arc from A to D), the
velocity increases. Once at position D, the bob will have a zero
displacement and a maximum velocity. The velocity is greatest when the
displacement is least. The animation at the right (used with the
permission of 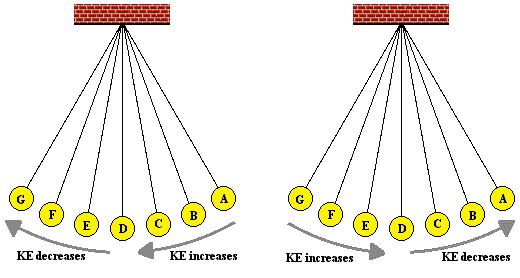


 Perhaps,
this observation of energy dissipation or energy loss is the
observation that triggers the "slowing down" comment discussed earlier.
In physics (or at least in the English language), "slowing down" means
to "get slower" or to "lose speed". Speed, a physics term, refers to
how fast or how slow an object is moving. To say that the mass on the
spring is "slowing down" over time is to say that its speed is
decreasing over time. But as mentioned (and as will be discussed in
great detail
Perhaps,
this observation of energy dissipation or energy loss is the
observation that triggers the "slowing down" comment discussed earlier.
In physics (or at least in the English language), "slowing down" means
to "get slower" or to "lose speed". Speed, a physics term, refers to
how fast or how slow an object is moving. To say that the mass on the
spring is "slowing down" over time is to say that its speed is
decreasing over time. But as mentioned (and as will be discussed in
great detail  An object that is in periodic motion - such as a mass on a spring, a pendulum or
An object that is in periodic motion - such as a mass on a spring, a pendulum or  An
object in periodic motion can have a long period or a short period.
For instance, a pendulum bob tied to a 1-meter length string has a
period of about 2.0 seconds. For comparison sake, consider the
vibrations of a piano string that plays the middle C note (the C
note of the fourth octave). Its period is approximately 0.0038 seconds
(3.8 milliseconds). When comparing these two vibrating objects - the
1.0-meter length pendulum and the piano string which plays the middle C note
- we would describe the piano string as vibrating relatively frequently
and we would describe the pendulum as vibrating relatively
infrequently. Observe that the description of the two objects uses the
terms frequently and infrequently. The terms fast and slow are not used since physics types reserve the words fast and slow
to refer to an object's speed. Here in this description we are
referring to the frequency, not the speed. An object can be in periodic
motion and have a low frequency and a high speed. As an example,
consider the periodic motion of the moon in orbit about the earth. The
moon moves very fast; its orbit is highly infrequent. It moves through
space with a speed of about 1000 m/s - that's fast. Yet it makes a
complete cycle about the earth once every 27.3 days (a period of about
2.4x105 seconds) - that's infrequent.
An
object in periodic motion can have a long period or a short period.
For instance, a pendulum bob tied to a 1-meter length string has a
period of about 2.0 seconds. For comparison sake, consider the
vibrations of a piano string that plays the middle C note (the C
note of the fourth octave). Its period is approximately 0.0038 seconds
(3.8 milliseconds). When comparing these two vibrating objects - the
1.0-meter length pendulum and the piano string which plays the middle C note
- we would describe the piano string as vibrating relatively frequently
and we would describe the pendulum as vibrating relatively
infrequently. Observe that the description of the two objects uses the
terms frequently and infrequently. The terms fast and slow are not used since physics types reserve the words fast and slow
to refer to an object's speed. Here in this description we are
referring to the frequency, not the speed. An object can be in periodic
motion and have a low frequency and a high speed. As an example,
consider the periodic motion of the moon in orbit about the earth. The
moon moves very fast; its orbit is highly infrequent. It moves through
space with a speed of about 1000 m/s - that's fast. Yet it makes a
complete cycle about the earth once every 27.3 days (a period of about
2.4x105 seconds) - that's infrequent.

 resting
position will result in a vibration. Even a large massive skyscraper is
known to vibrate as winds push upon its structure. While held fixed in
place at its foundation (we hope), the winds force the length of the
structure out of position and the skyscraper is forced into vibration.
resting
position will result in a vibration. Even a large massive skyscraper is
known to vibrate as winds push upon its structure. While held fixed in
place at its foundation (we hope), the winds force the length of the
structure out of position and the skyscraper is forced into vibration.
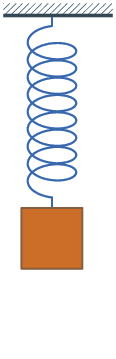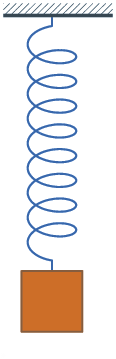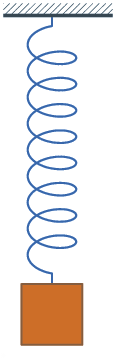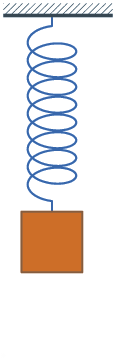 from
a spring. The mass hangs at a resting position. If the mass is pulled
down, the spring is stretched. Once the mass is released, it begins to
vibrate. It does the back and forth, vibrating about a fixed
position. If the spring is rotated horizontally and the mass is placed
upon a supporting surface, the same back and forth motion can be
observed. Pulling the mass to the right of its resting position
stretches the spring. When released, the mass is pulled back to the
left, heading towards its resting position. After passing by its
resting position, the spring begins to compress. The compressions of
the coiled spring result in a restoring force that again pushes
rightward on the leftward moving mass. The cycle continues as the mass
vibrates back and forth about a fixed position. The springs inside of a
bed mattress, the suspension systems of some cars, and bathroom scales
all operated as a mass on a spring system.
from
a spring. The mass hangs at a resting position. If the mass is pulled
down, the spring is stretched. Once the mass is released, it begins to
vibrate. It does the back and forth, vibrating about a fixed
position. If the spring is rotated horizontally and the mass is placed
upon a supporting surface, the same back and forth motion can be
observed. Pulling the mass to the right of its resting position
stretches the spring. When released, the mass is pulled back to the
left, heading towards its resting position. After passing by its
resting position, the spring begins to compress. The compressions of
the coiled spring result in a restoring force that again pushes
rightward on the leftward moving mass. The cycle continues as the mass
vibrates back and forth about a fixed position. The springs inside of a
bed mattress, the suspension systems of some cars, and bathroom scales
all operated as a mass on a spring system. 

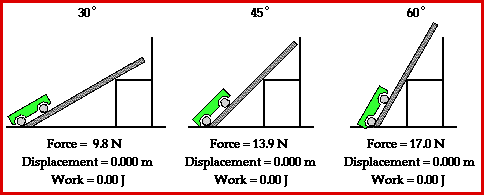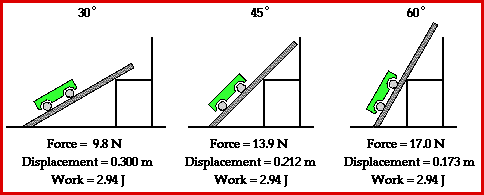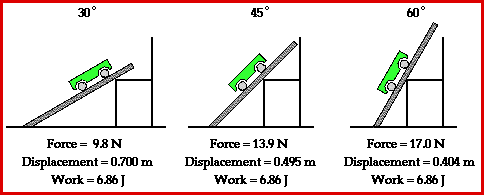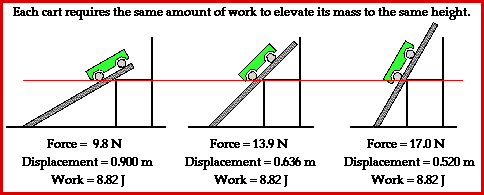
 This
situation can be simulated by use of a simple physics lab in which a
force is applied to raise a cart up an incline at constant speed to the
top of a seat. Three different incline angles could be used to represent
the three different paths up the mountain. The seat top represents the
summit of the mountain. And the amount of gasoline (or energy) required
to ascend from the base of the mountain to the summit of the mountain
would be represented by the amount of work done on the cart to raise it
from the floor to the seat top. The amount of work done to raise the
cart from the floor to the seat top is dependent upon the force applied
to the cart and the displacement caused by this force. Typical results
of such a physics lab are depicted in the animation below.
This
situation can be simulated by use of a simple physics lab in which a
force is applied to raise a cart up an incline at constant speed to the
top of a seat. Three different incline angles could be used to represent
the three different paths up the mountain. The seat top represents the
summit of the mountain. And the amount of gasoline (or energy) required
to ascend from the base of the mountain to the summit of the mountain
would be represented by the amount of work done on the cart to raise it
from the floor to the seat top. The amount of work done to raise the
cart from the floor to the seat top is dependent upon the force applied
to the cart and the displacement caused by this force. Typical results
of such a physics lab are depicted in the animation below.