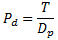AGMA Standard of Gear Design
A designed gear should meet following design criteria conforming to AGMA standards. It should have
- Enough mechanical strength to withstand force transmitted
- Enough surface resistance to overcome pitting failure
- Enough dynamic resistance to carry fluctuating loads
Design Inputs and Outputs in Gear Design
Following figure shows design inputs and outputs of a gear design
 |
| Fig.1 Input and output parameters for a gear design |
Various design output parameters are pictorially represented in following figure.
 |
| Fig.2 A general spur gear nomenclatures |
Design for space constrains
The designed gear system should fit within a space limit. So the
designer could say if he sums pitch diameters of the mating gears, it
should be less than or equal to allowable space limit as shown in figure
below.
 |
| Fig.3 Space constrain of gear design |
The blue rectangle represents space on which gear should get fit. One
can take 80% of width of this space as allowable width for gear design.
So following is the relation obtained by this condition.
We also know speed ratio of gears, this will lead to one more relation in terms of pitch circle diameters.
By solving above 2 equations simultaneously we can obtain pitch circle diameters of both the gears.
Determination of Number of Teeth - Interference
Here we will understand how to determine number of teeth on both the
gears. To do this we have to assume number of teeth on one gear(T1), say
the smaller gear. Now using the relation given below we can determine
number of teeth on other gear,T2.
So we got number of teeth on both the gears, but one should also check
for a phenomenon called interference if gear system has to have a smooth
operation. Interference happens when gear teeth has got profile below
base circle. This will result high noise and material removal problem.
This phenomenon is shown in following figure.
 |
| Fig.4 A pair of gear teeth under interference |
If one has to remove interference , the pinion should have a minimum number of teeth specified by following relation.
Where aw represents addendum of tooth. For 20 degree pressure
angle(which is normally taken by designers) aw = 1 m and bw = 1.2 m.
Module m, and pitch circle diameter Pd are defined as follows.
If this relation does not hold for a given case, then one has to
increase number of teeth T1, and redo the calculation. The algorithm for
deciding number of teeth T1 and T2 is shown below.
 |
| Fig.5 Flow chart to determine number of teeth on each gears |
Design for Mechanical Strength - Lewis Equation
Now the major parameter remaining in gear design is width of the gear
teeth, b. This is determined by checking whether maximum bending stress
induced by tangential component of transmitted load, Ft at the root of
gear is greater than allowable stress. As we know power transmitted,P
and pitch line velocity V of the gear Ft can be determined using
following relation.
Here we consider gear tooth like a cantilever which is under static
equilibrium. Gear forces and detailed geometry of the tooth is shown in
figure below.
 |
| Fig.6 Gear tooth under load |
One can easily find out maximum value of bending stress induced if all
geometrical parameters shown in above figure are known. But the
quantities t and l are not easy to determine, so we use an alternate
approach to find out maximum bending stress value using Lewis approach.
Maximum bending stress induced is given by Lewis bending equation as
follows.
Where Y is Lewis form factor, which is a function of pressure angle,
number of teeth and addendum and dedendum. Value of Y is available as in
form of table or graph. Using above relation one can determine value of
b, by substituting maximum allowable stress value of material in LHS of
equation. But a gear design obtained so will be so unrealistic, because
in this design we are considering gear tooth like a cantilever which is
under static equilibrium. But that's not the actual case. In next
session we will incorporate many other parameters which will affect
mechanical strength of the gear in order to get more realistic design.
A More Realistic Approach - AGMA Strength Equation
When a pair of gear rotates we often hear noise from this, this is
due to collision happening between gear teeth due to small clearance in
between them. Such collisions will raise load on the gear more than the
previously calculated value. This effect is incorporated in dynamic
loading loading factor, Kv value of which is a function of pitch line
velocity.
At root of the gear there could be fatigue failure due to stress
concentration effect. Effect of which is incorporated in a factor called
Kf value of which is more than 1.
There will be factors to check for overload (Ko) and load
distribution on gear tooth (Km). While incorporating all these factors
Lewis stregth equation will be modified like this
The above equation can also be represented in an alternating form (AGMA Strength equation) like shown below
Where J is
Using above equation we can solve for value of b, so we have obtained
all the output parameters required for gear design. But such a gear does
not guarantee a peacefull operation unless it does not a have enough
surface resistance.
Design for surface resistance
Usually failure happens in gears due to lack of surface resistance,
this is also known as pitting failure. Here when 2 mating surfaces come
in contact under a specified load a contact stress is developed at
contact area and surfaces get deformed. A simple case of contact stress
development is depicted below, where 2 cylinders come in contact under a
load F.
 |
| Fig.7 Surface deformation and development of surface stress due to load applied |
For a gear tooth problem one can determine contact stress as function of following parameters
If contact stress developed in a gear interface is more than a critical
value(specified by AGMA standard), then pitting failure occurs. So
designer has to make sure that this condition does not arise.