Uses of Second Law
Direction of a Process
Most important use of second law is to
determine direction of a process. First law of thermodynamics tells the
user only about energy transfer, it does not specify in which direction
energy transfer will happen for a given condition. Consider following
examples.According to first law hot tea can gain heat, mass can go up
and mixed gas can become unmixed spontaneously. It is 2nd law of
thermodynamics which comes in between and tells in which direction a
process is possible spontaneously.
 |
| Fig.1 Second law is used to determine in which direction above processes will happen spontaneously |
Well, you could argue that you can find out direction of all this
processes without using second law (from your intuition). Then what
about following process, a chemical reaction.
 |
| Fig.2 Second law can even check whether the chemical reaction above is spontaneous or not |
Can you say in which direction reaction will go spontaneously from your
intuition ? Using 2nd law you can predict even this, you can predict
whether the blue atoms and yellow atoms combine together to form a new
molecule spontaneously.
Maximum Possible Thermal Efficiency
Another main use of 2nd
law is in determining maximum possible thermal efficiency of a given
system. 2nd law of thermodynamics puts a limit for maximum performance a
system can achieve. For example you can find whats the maximum thermal
efficiency possible for a car engine or refrigerator just by knowing its
heat interaction temperatures.
Classical Statements of 2nd Law
Clausius Statement
According
Clausius statement heat cannot flow from a hot body to cold body
without any external work.This is depicted in following figure.
 |
| Fig.3 Clausius statement does not permit the process shown here |
Kelvin-Planck Statement
Accoriding to Kelvin-Planck
statement a heat engine cannot produce work without rejecting some heat
to the surrounding. This is depicted in following figure.
 |
| Fig.4 Kelvin-Planck statement does not premit the process shown in figure |
Clausius Inequality - 2nd Law in a Useful form for Engineers
Clausius and Kelvin-Planck are 2 classical statements of 2nd law,
but they are not in a form which is directly useful for engineers.Most
useful form of 2nd law is Clausius inequality, It states that cyclic
integral of dQ/T along boundary of a cycle will always be less than or
equal to zero.
Here temperature T should be in Kelvin.Right hand side of this equation
becomes zero when there is no irreversibility present in the cycle,
irreversibilities like friction or vertices. Consider following example,
a power production cycle.
 |
| Fig.5 Clausius inequality applied on a power plant cycle, dotted line represents boundary of the cycle |
Here there are 2 heat interactions in the cycle, one at condenser
represented by 'c' next is at boiler represented by 'b'. Assuming there
are no irreversibilities present and heat interactions are in uniform
temperature, then Clausius inequality reduces to
Concept of Carnot Engine
When heat interactions are happening
at uniform temperature and irrevesibilities in cycle are zero, such
cycle will give maximum possible thermal efficiency.This cycle is known
as Carnot cycle. In this aspect the power cycle we just discussed above
is an example of Carnot cycle. So thermal efficiency of such a cycle can
be written as
Or 2nd law states that a cycle which gives thermal efficiency more than
Carnot efficiency is impossible. If somebody approaches you claiming a
very high efficiency engine, with efficiency greater than Carnot
efficiency you can send him back immediately.
Second Law for a Process - Concept of Entropy
If you want to
apply 2nd law for a process the statements derived above which are for
cycles are not useful. Consider following cyclic processes, 1st cycle
passes through paths A & B and 2nd cycle passes through paths A
& C.
 |
| Fig.6 Two cyclic processes used to define 2nd law for a process, here process A same for both the cycles |
If there is no irreversibitly in the cycle Clausius inequality for the first cycle cycle can be written as
Similarly Clausius inequality for 2nd cycle can be written as
Comparing these two equations one can write
So irrespective of path taken integration of the quantity dQ/T for a
reversible process remains same. This is exactly how a property is
defined, properties are independent of path taken. We will call this
property
entropy, denoted by S.So for a reversible process change in entropy can be represented as
Second Law for an Irreversible Process
One can extend 2nd law equation derived for reversible process to an irreversible. In this case a term called
entropy production should be added to the equation.
Entropy production signifies degree of irreversibilities during the process. So entropy change equation for an irreversible process is
So there could be 2 components for entropy change in an actual process
- Entropy transfer - due to heat interaction
- Entropy production - due to effect of irreversibilites
Value of entropy transfer can be either positive or negative but value of entropy production is always positive.
Increase of Entropy Principle
Consider following case, where system is losing some heat to surroundings. We can approach this problem in 2 ways.
 |
| Fig.7 Two approaches in solving same problem, second approach states that entropy transfer of universe is zero |
In first approach we consider object as system, so system is losing some
entropy due to entropy transfer. In second approach we are considering
the object and surrounding of the object together as system, means we
are considering the universe together. In such an approach there will
not be any heat loss from it. Whatever heat interactions are happening
is within the universe. So there is no entropy transfer from universe.
The general entropy change equation will be simplified as
Since entropy production term is always positive, from above equation it
is clear that change of entropy of universe always positive or entropy
of universe always increases. This is increase of entropy principle. We
will do a sample problem to demonstrate increase of entropy principle.
Consider the following case, a hot tea which is in a surrounding whose
temperature is less than temperature of tea. Now the question is whether
the tea will gain heat or lose heat ?
 |
| Fig.8 Whether this tea will gain hear or lose heat ? |
First assume the tea is gaining 10J of heat, then change in entropy of universe is
Substituting values in it
This shows that entropy change of universe is negative, that is against
2nd law of thermodynamics. But if the tea loses 10J of heat this will
lead to increase in entropy of universe, which means this is a feasible
process.
Concept of Gibbs Free Energy
While using
increase of entropy principle
engineer has to calculate entropy change of surrounding also.In order
to over come this difficulty a new property is introduced -
Gibbs free energy.
 |
| Fig.9 Use of Gibb's free energy change in determining whether this chemical reaction is spontaneous or not |
Consider the example shown above, here we want to determine whether the
given chemical reaction will occur spontaneously. For this purpose we
have to determine entropy change of universe as we did in earlier case.
Here entropy change of system and enthalpy change of system are given,
so entropy change of surrounding is given by
So entropy change of universe is
This process is spontaneous if
Since T is always positive we can write process is spontaneous if
We will call L.H.S of this equation as another property called
Gibbs free energy. So in short a process is spontaneous if
Most of the time it is also convenient to talk in terms of Gibbs free
energy. When Gibbs free energy change of system is less than zero it
implies entropy change of universe is greater than zero.
Industrial Applications of 2nd Law
Second law of
thermodynamics is extensively used in industry to determine direction of
a process or a reaction. Most common method to check whether a reaction
is spontaneous is to find out change in Gibbs free energy. If this term
is negative for a reaction then the process is spontaneous.
Does Entropy Mean Disorder?
The
discussions we have done so far were in macroscopic point of view. But
there exists a whole different field of thermodynamics where things are
viewed microscopically, called as Statistical thermodynamics.
Boltzman relation is
considered to be one of the pillar statement of statistical
thermodynamics, at the same time it is one of the most controversial
too. According to this entropy, S and thermodynamic probability, w are
related by the relation
The term thermodynamic probability, w deserves special attention. It
represents total number of possible microscopic states available to a
system, it often referred to as disorder of the system. So according to
Boltzman relation as disorder of the system increases entropy increases,
or if during a process disorder of the universe increases that process
is spontaneous.But always remember statistical thermodynamics is not
free of controversies, especially
Boltzman relation. For an engineer thermodynamics in classical point of view is enough for his needs.

















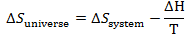




ليست هناك تعليقات:
إرسال تعليق