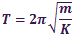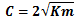A Simple Experiment to Understand Nature of Vibration
Consider
following spring-mass system. First spring is given a small initial
stretch second spring is given more stretch. If you measure time period
of oscillation for both the cases you can find it is same! Both are
having a time period of 6.28 s.
 |
| Fig.1 Different initial stretch is given to the same spring-mass system and time period is measured |
This is one big characteristic of vibrating systems, time period of
oscillation does not depend upon initial stretch you give, it is a
property of the system. More commonly used term used in vibrating world
is frequency, which is defined as follows.
Where T is time period of oscillation. Or one could say frequency of
oscillation is a property of the system. More precise term is
natural frequency,
since the system is made up of only stiffness and inertial components.
This is true even for a complicated system, say a bridge, chimney or an
electronic circuit. All of them has got a property called natural
frequency
Mathematical Analysis
One can do mathematical analysis of any
vibrating system with help of Newton's 2nd law of motion. Newton's
second law motion when applied on mass lead to following differential
equation.
This equation has got many solutions, solution of highest significance is given below.
Where A is initial stretch given to the spring. Graphically it is represented as shown in below.
 |
| Fig.2 Graphical representation of motion of spring-mass system with time |
Where Y is measured downward from equilibrium line, a line where at
which gravitational force and spring force are balanced (represented by
blue dotted line). Time period of oscillation and angular frequency can
be derived from equation above as
So for a simple spring-mass system frequency of vibration is a function
of mass and spring constant.If you substitute values of spring constant
and mass of previous experiment in above equation time period of
vibration can be obtained as 6.28s.
Effect of Damping on Vibration
You can notice that vibration
of mass continues forever in previous case, it never dies out. But this
is not a practical case, what do you see in practice is something like
this.
Amplitude of oscillation decreases with time and it finally dies out.
Here we have to consider effect of air viscous force on mass in order
to simulate this problem more accurately. Damping causes continuous
energy loss to the system, as system loses its energy amplitude of
oscillation decreases.
 |
| Fig.3 Amplitude vibration decreases in an actual case due to effect of air viscous force |
Forces acting on mass in this case shown in figure below in blue arrows.
Here spring force and viscous(damping) forces are acting on the mass,
damping force is proportional velocity of mass with opposite sign of
velocity. Effect of air viscous force can be represented as a single
viscous dash port as shown.
 |
| Fig.4 Forces acting on a damped vibration case |
Mathematical solution of this problem can be obtained by applying
Newton's 2nd law of motion to the system. The differential equation so
obtained will be
It has got one more term compared to simple spring-mass system case, a term to incorporate viscous force on mass.
Critical and Over Damping
Now let us use a highly viscous fluid around the mass instead of air.
Here you can find that vibration dies out much faster and tendency of
oscillation has decreased. As you increase viscosity of fluid further
tendency for oscillation further decreases. So there will be a limiting
viscosity where oscillatory behavior of mass completely disappears. This
phenomenon is known as critical damping, where the mass goes back to
its equilibrium position without any oscillation.
 |
| Fig.5 As
viscosity of surrounding fluid is increased tendency for oscillation
decreases and finally a case with no oscillation is reached |
Coefficient of viscosity required for achieving critical damping is given by
You can further increase viscosity of surrounding, even above critical
damping limit and notice that here also mass goes to equilibrium
position without any oscillation. This condition is known as overdamped.
Effect of External Force - Resonance
When an oscillating
external force is applied on mass nature of vibration will change
dramatically. Here oscillating frequency will be same external force
frequency, it is not related natural frequency of the system. Amplitude
of the oscillation is not the initial stretch given by the user, but it
will be strong function of external frequency and natural frequency.
Amplitude of oscillation will become very high when external frequency
and natural frequency values are very close.If external force frequency
is same as natural frequency of material it will result in a phenomenon
called resonance, where amplitude of oscillations become so high and it
will eventually result in damage of material.
Industrial Applications
- The Intriguing problem of Chimney Collapse
Have you ever noticed rings at top of a chimney? What does it signify? We
will go through an incident which happened almost 100 years back. A
chimney which conforms to mechanical strength requirement was erected in
England in 1900s. But surprising engineers who built it,the structure
collapsed one day. An enquiry was launched to investigate what went
wrong in design of the chimney. After a detailed research the enquiry
commission came up with a startling report. Their conclusion was like
this.
The collapse happened because designers did not consider
effect of vibration / resonance of chimney. When wind blows across
chimney during a particular wind speed range a phenomenon called Vortex
shedding happens behind the chimney, here flow vortexes appear and
disappear at a particular frequency. This will induce fluctuating force
of same frequency on chimney. If frequency of vortex shedding is same as
natural frequency of material of construction this will lead to
resonance. At resonance amplitude of oscillation becomes so large that
structure finally collapses. That exactly what happened for the chimney.
So
what could be a solution for this danger. The obvious answer is prevent
Vortex shedding phenomenon, so that the chimney will not vibrate. And
the rings you see on chimney are vortex breakers, which will distract
the flow and spoil vortex formation behind chimney.
Why do they spend lot of time on mass balancing?
How to build a career in field of Vibration?
Excited
about field of vibration? Do you want a build career in this filed ? If
answers to these questions are Yes, then an exciting world of NVH
(Noice,Vibration & Harshness) is awaiting you. There are 2 different
career streams available according to your interest
Experimental analysis and Development
- Balancing of rotating components
- Noise testing
FEA based simulation and Development
You can simulate almost all the things you do experimentally in
computers using FEA. So it is obvious that you have to have a strong
knowledge in Finite Element Analysis in order to enter this job domain.
Anyway before you start dreaming on this careers first thing you have to
do is gain more in-depth knowledge on vibration. Hope from this website
you got a good introduction to this filed. Now its time to go through
some standard text books and learn more on this field.